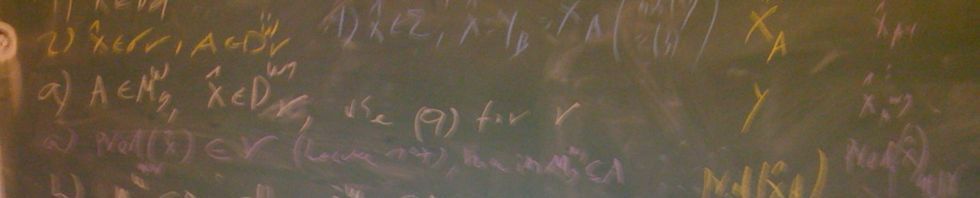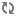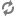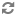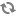These are the slides of a contributed talk given at the Logic in Hungary 2005 meeting (Budapest, 5–11 August 2005).
Talk Title: On the consistency strength of the Milner-Sauer Conjecture
Abstract: In their paper from 1981, after learning about Pouzet‘s theorem that any poset of singular cofinality mush contain an infnite antichain, Milner and Sauer came up with the following conjecture:
Every poset $\mathbb P$ of singular cofinality, must contain an antichain of size $\text{cf}(\text{cf}(\mathbb{P})).$
By the work of Milner-Pouzet, Milner-Prikry, Hajnal-Sauer, the conjecture is known to be consistent, e.g, it follows from GCH and other GCH-type assumptions.
We here establish that the conjecture has high consistency strength by showing that it already follows from Shelah’s Strong Hypothesis and other SSH-type assumptions.
Downloads:
