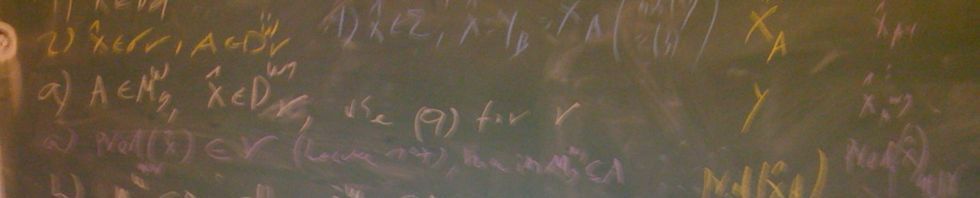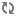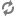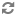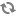This talk was given at the 2006 Annual Conference of the Israel Mathematical Union (Neve Ilan, 25-26 May 2006).
Talk Title: The Milner-Sauer conjecture and covering numbers
Abstract: In their paper from 1981, after learning about Pouzet‘s theorem that any poset of singular cofinality mush contain an infnite antichain, Milner and Sauer came up with the following conjecture:
Every poset $\mathbb P$ of singular cofinality, must contain an antichain of size $\text{cf}(\text{cf}(\mathbb{P})).$
In a previous paper, we proved that the conjecture follows from Shelah’s Strong Hypothesis, thus yielding a large cardinals consistency strength for the conjecture. Here, we shall improve this result and present a condition in terms of covering numbers that already implies the Milner-Sauer conjecture. This condition is very weak, and there is no known model of set theory that satisfies the negation of this condition.
Downloads:
