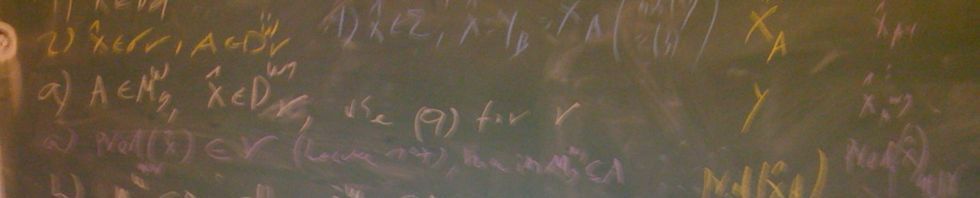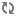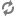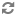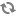A topological reflection principle equivalent to Shelah’s strong hypothesis

Abstract: We notice that Shelah’s Strong Hypothesis (SSH) is equivalent to the following reflection principle:

Suppose $\mathbb{X}$ is an (infinite) first-countable space whose density is a regular cardinal, $\kappa$.
If every separable subspace of $\mathbb{X}$ is of cardinality at most $\kappa$, then the cardinality of $\mathbb{X}$ is $\kappa$.

Downloads:

Citation information:

A. Rinot, A topological reflection principle equivalent to Shelah’s Strong Hypothesis, Proc. Amer. Math. Soc., 136(12): 4413-4416, 2008.

Update:

In a more recent paper, the arguments of the above paper were pushed further to show that SSH is also equivalent to the following:

Suppose $\mathbb{X}$ is a countably tight space whose density is a regular cardinal, $\kappa$.
If every separable subspace of $\mathbb{X}$ is countable, then the cardinality of $\mathbb{X}$ is $\kappa$.