I gave a colloquium talk at Bar-Ilan University on November 10, 2013.
Title: Forcing as a tool to prove theorems
Abstract:
Paul Cohen celebrated solution to Hilbert’s first problem showed that the Continuum Hypothesis is independent of the usual axioms of set theory. His solution involved a new apparatus for constructing models of set theory – the method of forcing. As Cohen predicted, the method of forcing became very successful in establishing the independence of various statements from the usual axioms of set theory. What Cohen never imagined, is that forcing would be found useful in proving theorems (that is, implications).
In this talk, we shall motivate the forcing machinery, and then present a collection of results that were proved using the method of forcing.
The talk was intended for a general audience, and comments are very welcome.
Downloads:


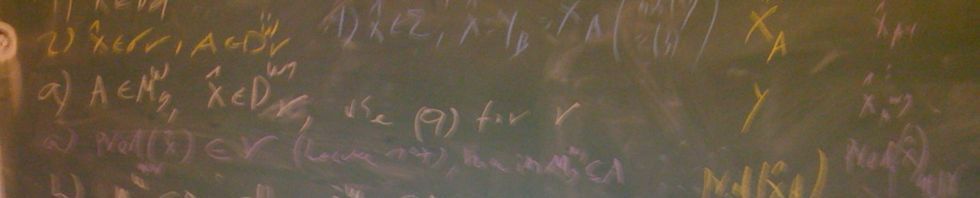
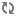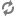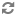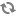
In A nonconstructible $\Delta^1_3$ set of integers, the following is proved by Robert Solovay using forcing:
Theorem. Assuming the existence of a Ramsey cardinal, there is a $\Delta^1_3$ set of sets of integers, X, which is not constructible from any set of integers A.
The following is stated about the proof of the above theorem:
Thanks for this finding, Mohammad! It is an amazing fact that already in 1967, Solovay proved a ZFC theorem using forcing.
p.s.
Here is an interesting quote of Shelah (from here):
Dear Assaf,
The only forcing free proof of the Gitik-Shelah theorem (forcing with a sigma ideal cannot be isomorphic to a product of Cohen and random forcings) that I used in the rational distance result is probably due to Burke and Fremlin as I read here:
https://www.essex.ac.uk/maths/people/fremlin/n96j01.ps
Kamburelis’ paper seems to cover the cases of random and Cohen forcings but not the product. Do you know another published version of the Cohen times random case?
Hi Ashutosh,
I very much like this theorem of yours concerning irrational distances!
Thanks for your feedback – I corrected the slides.
Next time I see Gitik, I will ask him about known forcing-free proofs of the Cohen times random case. I asked him: he is not aware of additional forcing-free proofs.