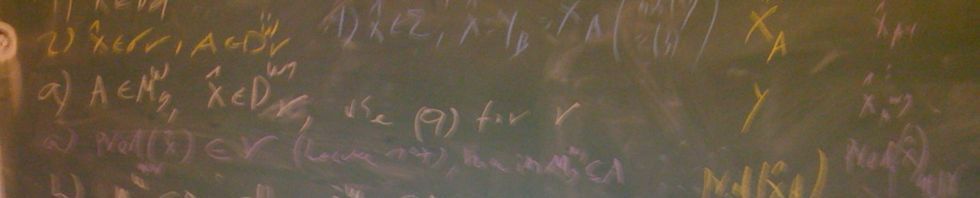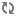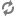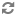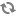Abstract. It is proved that in Godel’s constructible universe, for every successor cardinal $\kappa$, there exist graphs $\mathcal G$ and $\mathcal H$ of size and chromatic number $\kappa$, for which the tensor product graph $\mathcal G\times\mathcal H$ is countably chromatic.
with Sauer and Hajnal, Budapest, August 2005
Downloads:
Citation information:
A. Rinot, Hedetniemi’s conjecture for uncountable graphs, J. Eur. Math. Soc., 19(1): 285-298, 2017.
