Joint work with Tanmay Inamdar.
Abstract. We continue our study of Sierpinski-type colourings. In contrast to the prequel paper, we focus here on colourings for ideals stratified by their completeness degree. In particular, improving upon Ulam’s theorem and its extension by Hajnal, it is proved that if
A second focus here is the feature of narrowness of colourings, one already present in the original theorem of Sierpinski. This feature ensures that a colouring suitable for an ideal is also suitable for all superideals possessing the requisite completeness degree. It is proved that unlike successors of regulars, every successor of a singular cardinal admits such a narrow colouring.
Downloads:
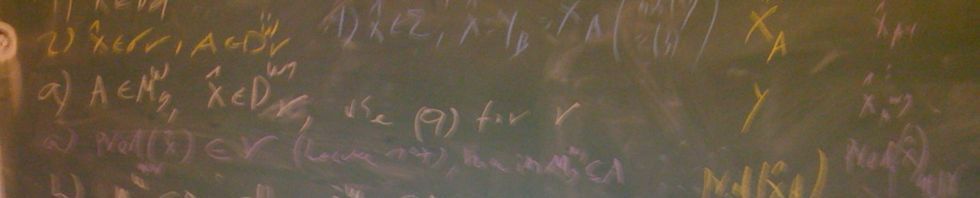
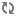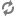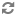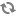
Submitted to Algebra Universalis, March 2022.
Accepted, December 2023.