Abstract. It is proved that for every uncountable cardinal $\lambda$, GCH+$\square(\lambda^+)$ entails the existence of a $\text{cf}(\lambda)$-complete $\lambda^+$-Souslin tree.
In particular, if GCH holds and there are no $\aleph_2$-Souslin trees, then $\aleph_2$ is weakly compact in Godel’s constructible universe, improving Gregory’s 1976 lower bound.
Likewise, if GCH holds and there are no $\aleph_2$ and $\aleph_3$ Souslin trees, then the Axiom of Determinacy holds in $L(\mathbb R)$.
p.s.
This also answers Question 9 from this survey paper in the affirmative (see also p. 261 of the Kanamori-Magidor 1978 article).
Downloads:
![[No arXiv entry]](/design/002_arxiv_dis.png "No arXiv entry") |
Citation information:
A. Rinot, Higher Souslin trees and the GCH, revisited, Adv. Math., 311(c): 510-531, 2017.
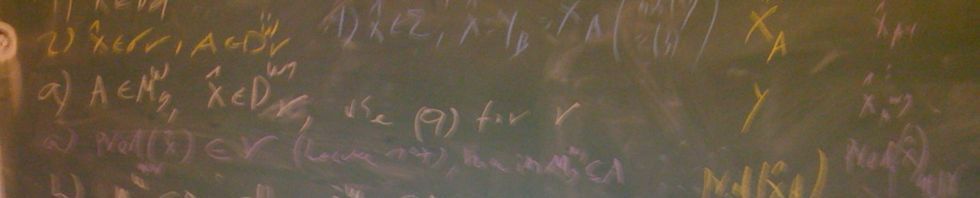
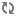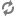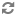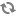
It seems to be very nice. I have a question:
Assume $kappa$ is Mahlo and let $L[G]$ be the generic extension of $L$ obtained by Mitchell forcing to make $2^{\aleph_0}=\aleph_2=\kappa.$ Do you know if there are $aleph_2$-Souslin trees in $L[G].$
I assume the answer is yes. Unfortunately Theorem D of your paper does not apply. Also, do you know if the assumption $\lambda\geq \beth_\omega$ is essential in Theorem D.
Thanks, Mohammad.
Last week, Yair Hayut asked me the same question, but I don’t know the answer. The approach of the paper does not apply as witnessed by Corollary 2.9.
Update: Yair showed that the answer is affirmative.
Same goes to Theorem D: by Corollary 2.5, the approach will not come into play.
It is surprising that if we apply Mitchell’s construction above $\beth_\omega,$
then we know the answer by your results, but we don’t know the answer for smaller cardinals!
I doubt the answer would be any different, yet, generally speaking, there are plenty of witnesses to the (two) fact(s): it is possible to postpone the consequences of fine structure for a while, but not forever :).
In comparison with the case of Aronszajn trees and tree property in consecutive cardinals, what is the technical issue with expanding the results of theorem C for non-existence of Suslin trees in more than two consecutive cardinals?
I guess the huge jump in the consistency strength between the case of $aleph_2$ (Theorem A) and $aleph_2,aleph_3$ (Theorem C) in the presence of $GCH$, which is as wide as the gap between weakly compacts and holding $AD$ in $L(mathbb{R})$, suggests that going any further in this direction might cause some inconsistencies. Is this intuition true or there are some intuitive arguments that suggest the possibly of getting far better consistency results in this direction?
PFA (that follows from a supercompact, and is consistent with GCH-CH) entails the failure of $\square(\kappa)$ for all regular $\kappa\ge\aleph_2$, making this paper’s approach inapplicable.
In fact, by the last corollary of Section 1 in here, PFA is consistent with the existence of $\kappa$-Souslin trees for every regular $\kappa\ge\aleph_3$.
Thank you Assaf, for the explanation. By the way is there any possible direction in which you want to follow as the continuation of the results in this interesting paper?
yes. The approach of the above paper proved fruitful for successor cardinals, and proved unfruitful for inaccessibles (Proposition 2.10). My next project involves a different approach that allows to tackle the inaccessbiles.
I wonder to know what is your belief about the main open problem. Do you think $GCH$ alone gives the existence of $\aleph_2$-Souslin trees?
At this point in time, the chances seem even to me.
What about some “slightly weaker” forms of “existence of $\aleph_2$-Souslin trees”? Does $GCH$ alone imply any of them to be a basis for thinking about the stronger case? Do you have any example in mind?
Are you correct with your note about PFA. I think it implies tree property at $\aleph_2,$
in particular there are no $\aleph_2$-Souslin trees. But for cardinals bigger than $\aleph_2$, yes it is true.
Thanks. Indeed, I meant $\aleph_3$.
Pingback: Square principles | Assaf Rinot
Pingback: More notions of forcing add a Souslin tree | Assaf Rinot
Submitted to Advances in Mathematics, May 2016.
Accepted, March 2017.