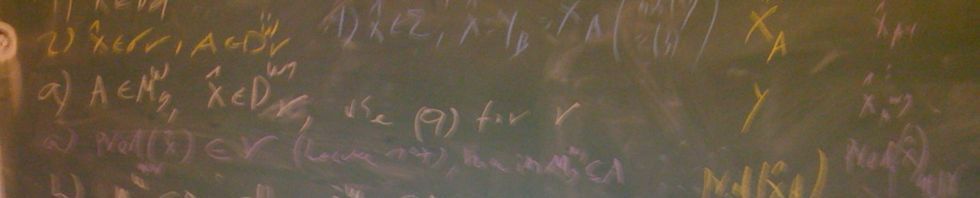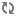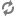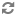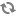These are the slides of a talk I gave at the Young Researchers in Set Theory 2011 meeting (Königswinter, 21–25 March 2011).
Talk Title: Around Jensen’s square principle
Abstract: Jensen‘s square principle for a cardinal $\lambda$ asserts the existence of a particular ladder system over $\lambda^+$.
This principle admits a long list of applications including the existence of non-reflecting stationary sets, and the existence of particular type of trees.
In this talk, we shall be concerned with the weaker principle, weak square, and the stronger principle, Ostaszewski square, and shall study their interaction with the classical applications of the square principle.
We shall isolate a non-reflection principle that follows from weak square, and discuss tree constructions based on Ostaszewski squares.
We shall present a rather surprising forcing notion that may (consistently) introduce weak square, and discuss a coloring theorem for pairs of ordinals, based on minimal walks along Ostaszewski squares.
Downloads:
Updates:
The first open problem from this presentation (slide 35) has been resolved. The solution may be found in here.
